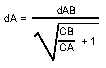Rural (Normative) Service Areas / Isolines

In order to determine the normative service area a radius is drawn around a settlement (village, town or urban centre). The radius represents the service facility according to the distance. For example, the service radius of a small health clinic maybe 5 km while that of a district hospital could be as much as 40 km.

Step 1:

Determine the important services that should be spatially depicted

Step 2:

Determine the acceptable service area for the specific service

Step 3:

Draw a radius around the settlement for each respective service that the planner wishes to depict.

Similar process can be undertaken for isolines. Isolines represent distances to services in a similar way to the normative service areas described above.

Map 1: Example of normative radius of a service area for a selected facility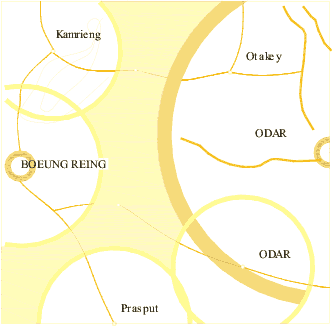

Possible forms of interpretation rural service centres:

• A possibility may exist to extend the service area by improving the transportation network
• There is a need to also examine whether or not the settlements offer sufficient capacity to cover the expected additional demand for goods and services
• The population outside of the service area may or may not fulfil the necessary threshold values required for a new rural centre or in order to be able to upgrade existing centres to higher order service centres
• Projections into the future may indicate that the threshold values maybe achieved at a later stage, this should be determined when this is likely to happen.
• The overall carrying capacity for the area maybe limited, the number of people living in the area is already at the limited in which case the expansion or development of a new centre cannot be justified.
• It is important, where possible, to select the most suitable settlement to be upgraded in terms of service provision and accessibility

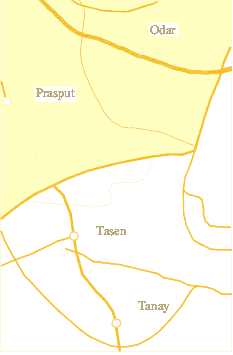
Map 2: Mapping of areas outside effective isoline of rural centres

Accessibility analysis

According to the gravitation hypothesis, it is assumed that inhabitants living at any point between two settlements A and B will be attracted to the towns accordance with the relative attractiveness of the towns and inversely with the distance.

Step 1:

Identify all the settlements to be analysed, including the neighbouring settlements.

Step 2:

Identify the distance (in km) to each settlement (d). For this it is possible to use the results of the distance matrix method.

Step 3:

Determine the functional index (C). The results of the functional index method should be used.

Step 4:

Compute the break even point (km)

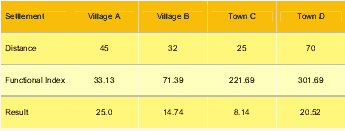
Table 1: Results of calculation (example only)

Step 5:

Alternatively it is possible to use the population instead of the functional index.

Step 6:

The alternative model calculation would be:

Table 2: Results of calculation (example only)

Map 3: Mapping of service area (example only)